Fractals en wiskunde

Hieronder volgt een korte en basale uitleg van 4 aspecten van fractals die mij enig inzicht hebben gegeven over de werking er van.

Fractals, wiskunde en 4 typische dingen over de Mandelbrot formule

Uitgaande van de basisformule (van Julia/Mandelbrot) zijn er vier basis dingen van belang om de achterliggende wiskunde te kunnen begrijpen :

• De werking van de formule; het iteratieve (zichzelf herhalend) aspect en het beslissingscriterium.
• Hoe een fractal geplot/geprint/afgebeeld kan worden op een assenstelsel, maar niet de gewone met de x en de y as, maar op het complexe vlak.
• En dit laatste impliceert dat er gewerkt wordt met complexe of imaginaire getallen.
• Tenslotte een korte uitleg over de relatie tussen de Mandelbrot en de Julia set.

De formule, interaties en imaginaire getallen

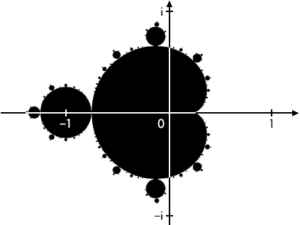
Het doel van de formule Z _n+1 = Z² + C is te bepalen welke uitkomsten van de formule wél en welke níet tot de Mandelbrot set behoren. De Mandelbrot set is te zien als de geplotte of afgebeelde fractal en omvat alle punten die er onderdeel van uit maken. Het criterium hierbij is de uitkomst van de formule. En hier komt het iteratieve aspect van de formule in beeld. Iteratief betekent niet anders dan dat het resultaat van de berekening wordt gebruikt als nieuwe invoer in dezelfde formule. In principe kun je dit dus eindeloos herhalen.

Het criterium

Terug naar het criterium. Als op basis van de gekozen waarde van C, waarbij Z₀ = 0  de uitkomst steeds groter wordt, behoort deze waarde niet tot de Mandelbrot set. Als anderzijds de waarde van Z _n steeds dichter bij een bepaalde, specifieke waarde komt, de attractor, dan behoort ze wél tot de Mandelbrot set en is dus (in het plaatje) zwart afgebeeld.

In een formule met uitsluitend ‘normale’ getallen is de oplossing heel simpel. Met een resultaat van boven de 1 worden alle volgende uitkomsten steeds groter; en omgekeerd, blijven de resultaten kleiner dan 1 dan worden volgende uitkomsten steeds kleiner.

Imaginaire getallen

De formule echter maakt gebruik van complexe getallen en dat maakt het net even anders. Het imaginaire getal i is gedefinieerd als i = √-1 of anders uitgedrukt:  i² = -1. Met reële getallen is voor i geen oplossing omdat het kwadraat van een willekeurig getal altijd positief is. Wat voor getal i eigenlijk is, is dan ook moeilijk voor te stellen. Maar dit belet wiskundigen niet om er toch mee te rekenen.

Een paar voorbeelden om te rekenen met imaginaire getallen

Stel dat je de wortel van -1 wilt berekenen. Je weet dat de wortel van -1 niet bestaat in de reële getallen, maar je kunt het wel uitdrukken als een imaginaire eenheid i. Dus √-1 = i.

Zo kan de berekening van √-4  geschreven worden als √(-1) x √4 = i x 2 = 2i.

Een ander voorbeeld zou kunnen zijn om de som van twee complexe getallen te berekenen, bijvoorbeeld (3 + 2i) + (4 – i). Dit doen we door de reële delen bij elkaar op te tellen en de imaginaire delen bij elkaar op te tellen. Dus (3 + 4) + (2i – i) = 7 + i.

Complexe getallen en het complexe vlak

Een voorbeeld van een complexe getal, Z en C uit de formule, is 4 + 0,5i.  Hier is 4 het reële deel en 0,5i het imaginaire deel. Het getal kan nu als een punt op het complexe vlak worden weergegeven in de vorm van coördinaten (4 , 0,5i).

Grappig hierbij is de vraag of de Mandelbrot set samenhangend is of dat hij bestaat uit losse punten. Want hoe kun je nu zeker weten dat alle punten in het gehele vlak bij de Mandelbrot set behoren, als je ze stuk voor stuk moet berekenen?

Een rekenvoorbeeld

Een rekenvoorbeeld bij het berekenen van de Mandelbrot fractal Z _n+1 = Z² + C:

Je kiest een complex getal C uit het complexe vlak, bijvoorbeeld C = 2 + 0,5i en begint met Z ₀ = 0. Je past de formule Z _n+1 = Z _n + C herhaaldelijk toe om een rij van complexe getallen te krijgen.

Z ₁ =Z ₀² + C = 0² + (2 + 0,5i) = 2 + 0,5i

In de volgende iteratie is Z ₂ = (2 + 0,5i)² + 2 + 0,5i

Kwadratering van een complex getal

(Z ₂)² = (2 + 0,5i)² = 2² +  2 * 0,5i + 2 * 0,5i + 0,5² + i²  = 4 + i + i + 0,25 * i² of 4 + 2i + 0,25 * i² . Gezien i² = -1, wordt dit 4 + 2i – 0,25 = 3,75 + 2i

Z ₂ = Z ₁² + C dus Z ₂ = 3,75 + 2i  + 2 + 0,5i = 5,75 + 2,5i . De trend naar steeds hogere waardes lijkt zichtbaar te worden.

Z ₃ = Z ₂² + C = (5,75 + 2.5i)² + (2 + 0,5i) = 33,0625 + 5,75 * 2,5i + 5,75 * 2,5i + 6,25i² +  ( 2 + 0,5i) =

33,0625 + 14,375i + 14,375i – 6,25 + 2 + 0,5i  = 28,8125 + 29,25i

De rij van Z _n wordt steeds groter  naarmate n toeneemt, dus het getal C = 2 + 0.5i behoort niet tot de mandelbrot fractal.

Een ander voorbeeld

C = -1 (+ 0i)

Z ₁ = Z ₀² + C = 0² + (-1) = -1
Z ₂ = Z ₀² + C = (-1)² + (-1) = 0
Z ₃ = Z ₀² + C = (0)² + (-1) = -1
Z ₄ = Z ₀² + C = (-1)² + (-1) = 0

De rij van Z _n is in dit geval periodiek met periode 2, dus het getal C behoort wel tot de Mandelbrot fractal.

.. en dan komt alles samen

Om de mandelbrot fractal te tekenen, moet je voor elk punt in het complexe vlak bepalen of het tot de fractal behoort of niet. Dit kan door een maximum aantal iteraties in te stellen, bijvoorbeeld 100, en te kijken of de rij van Z _n binnen een bepaalde grens blijft, bijvoorbeeld |Z _n| < 2. Als dat zo is, dan krijgt dat punt een bepaalde kleur, bijv. zwart en anders krijgt het een andere kleur afhankelijk van het aantal iteraties dat nodig was om de grens te overschrijden. Hier ligt de ruimte voor creativiteit.

Verbinding tussen de Mandelbrot en Julia set

Alle complexe getallen die deel uit maken van de Mandelbrot set, hebben een overeenkomstige Julia set. Of anders gezegd; elk complex getal uit de Mandelbrot set geeft een iets andere fractal in de Julia set, zie de afbeelding. Voor beide sets wordt dezelfde formule gebruikt, maar er is een verschil. Voor de Mandelbrot set wordt voor een gekozen punt (C, waarbij de eerste Z = 0) gekeken of dit wel dan niet tot de set behoort; de Julia set neemt het gekozen complexe getal als uitgangspunt en wordt gekeken welke andere (complexe) getallen hiertoe behoren. Dit Youtube filmpje legt het misschien helderder uit; www.youtube.com/watch?v=mg4bp7G0D3s

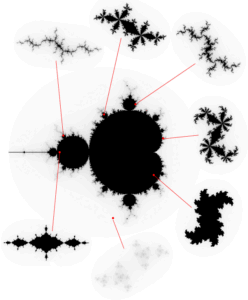Paul Bourke – julia_mandel

Op het internet zijn voor de liefhebber talloze filmpjes en pagina’s met uitleg over tal van aspecten van fractals te vinden. Een aantal die ik zelf verhelderend of bijzonder vond staan op de Info en Links pagina.